3. Methods in UCSD UQ Engine

3.1. Transitional Markov chain Monte Carlo

TMCMC is a numerical method used to obtain samples of the target posterior PDF. This algorithm is flexible, applicable in general settings, and parallelizable. Thus, it can be used to effectively sample the posterior PDF, when the likelihood function involves a computationally expensive FE model evaluation, using high-performance computing (HPC) resources.

In Bayesian inference, the posterior probability distribution of the unknown quantities, represented by the vector \(\mathbf{\theta}\), is obtained by applying Bayes’ rule as follows:

(3.1.1)\[p (\mathbf{\theta \ | \ y}) = \frac{p (\mathbf{y \ | \ \theta}) \times p(\mathbf{\theta})}{\int p (\mathbf{y \ | \ \theta}) \times p(\mathbf{\theta}) \ d\mathbf{\theta}}\]

The idea behind TMCMC is to avoid sampling directly from the target posterior PDF \(p(\mathbf{\theta \ | \ y})\), but to sample from a series of simpler intermediate probability distributions that converge to the target posterior PDF. To achieve this, the TMCMC sampler proceeds through a series of stages, starting from the prior PDF until the posterior PDF. These intermediate probability distributions (called tempered posterior PDFs) are controlled by the tempering parameter \(\beta_j\) as

(3.1.2)\[p(\theta|y)_j \propto p(y | \theta)^{\beta_j} \times p(\theta); \quad j = 0, 1, \ldots, m; \quad 0 = \beta_0 < \beta_1 < \ldots < \beta_m = 1\]

Index \(j\) denotes the stage number, \(m\) denotes the total number of stages, and \(p (\mathbf{\theta \ | \ y})_j\) is the tempered posterior PDF at stage \(j\) controlled by the parameter \(\beta_j\). At the initial stage \((j = 0)\), parameter \(\beta_0 = 0\), the tempered distribution \(p(\mathbf{\theta \ | \ y})_{j=0}\) is just the prior joint PDF \(p(\theta)\). The TMCMC sampler progresses by monotonically increasing the value of \(\beta_j\), at each stage \(j\), until it reaches the value of 1. At the final stage \((j = m)\), parameter \(\beta_m = 1\), the tempered distribution \(p(\mathbf{\theta \ | \ y})_{j = m}\) is the target posterior joint PDF \(p(\mathbf{\theta \ | \ y})\).

TMCMC represents the tempered posterior PDF at every stage by a set of weighted samples (known as particles). TMCMC approximates the \(j^{th}\) stage tempered posterior PDF \(p(\mathbf{\theta \ | \ y})_j\) by weighing, resampling, and perturbing the particles of the \(j-1^{th}\) stage intermediate joint PDF \(p(\mathbf{\theta \ | \ y})_{j-1}\). For details about the TMCMC algorithm, the interested reader is referred to Ching and Chen [Ching2007], Minson et. al. [Minson2013].

Ching2007

10. Ching and Y.-C. Chen, “Transitional Markov Chain Monte Carlo Method for Bayesian Model Updating, Model Class Selection, and Model Averaging”, Journal of Engineering Mechanics, 133(7), 816-832, 2007.

Minson2013

19. 5. Minson, M. Simons, and J. L. Beck, “Bayesian Inversion for Finite Fault Earthquake Source Models I-Theory and Algorithm”, Geophysical Journal International, 194(3), 1701- 1726, 2013.

3.2. Bayesian Inference of Hierarchical Models

Consider for model calibration a dataset consisting of experimental results on test specimens of the same kind. Let \(\mathbf{y}_i\) denote the measured output response of the \(i^{th}\) specimen in the dataset \(\mathbf{Y} = \{\mathbf{y}_1, \mathbf{y}_2, ..., \mathbf{y}_{N_s}\}\) where \(N_s\) designates the number of specimens. Let \(\theta_i\) be the model parameter vector corresponding to the \(i^{th}\) specimen, where \(n_\theta\) denotes the number of model parameters. For the \(i^{th}\) specimen, the output response \(\mathbf{y}_i\) can be viewed as a function of \(\theta_i\) through the model \(\mathbf{h}\) and the following measurement equation:

(3.2.1)\[\mathbf{y}_i = \mathbf{h}(\theta_i) + \mathbf{w}_i\]

where \(\mathbf{w}_i\) denotes the discrepancy between the response predicted by the model parameterized with \(\theta_i\), i.e., \(\mathbf{h}(\theta_i)\), and the experimental output response \(\mathbf{y}_i\); \(\mathbf{w}_i\) is termed the prediction error. With the measurement equation in (3.2.1), the sources of real-world uncertainties such as the measurement noise during data collection and model form error are lumped and accounted for in the prediction error (also called noise) term \(\mathbf{w}_i\) (i.e., \(\mathbf{w}_i\) is also a proxy for model form error). In quoFEM, it is assumed that the prediction error is a zero-mean Gaussian white noise, thus,

(3.2.2)\[\mathbf{w}_i \sim N(0, (\sigma_i^w)^2 \times I_{n_{\mathbf{y}_i} \times n_{\mathbf{y}_i}})\]

where \(\sigma_i^2\) denotes the variance of the prediction error \(\mathbf{w}_i\).

With the assumptions made in (3.2.1) and (3.2.2), \(\mathbf{y}_i\) is Gaussian and centered at the model response \(\mathbf{h}(\theta_i)\), with a diagonal covariance matrix equal to \(\sigma_i^2 \times \mathbf{I}_{n_{\mathbf{y}_i} \times n_{\mathbf{y}_i}}\) i.e.,

(3.2.3)\[p(\mathbf{y}_i | \theta_i, \sigma_i^2) = N(h(\theta_i), \sigma_i^2 \times \mathbf{I}_{n_{\mathbf{y}_i} \times n_{\mathbf{y}_i}})\]

In the UCSD_UQ engine, hierarchical Bayesian modeling is used to account for specimen-to-specimen variability in the parameter estimates. In the hierarchical Bayesian modeling realm, the parameter vectors \(\theta_1, \theta_2, \ldots, \theta_{N_s}\) are considered as mutually statistically independent and identically distributed (s.i.i.d) random variables following a PDF \(p(\theta | \eta)\). This is the PDF of the parent distribution, which represents the aleatory specimen-to-specimen variability.

The objective of hierarchical Bayesian inference is to jointly estimate the model parameters \(\theta_i\) for each specimen i (along with its prediction error variance \(\sigma_i^2\)) as well as the hyperparameters \(\eta\) of the parent distribution of the set \(\theta_i (i = 1, \ldots, N_s)\).

Making use of the experimental results for a single specimen, \(\mathbf{y}_i\), Bayes’ theorem for all parameters to be inferred from this specimen can be written as

(3.2.4)\[p(\theta_i, \sigma_i^2, \eta | \mathbf{y}_i) \propto p(\mathbf{y}_i | \theta_i, \sigma_i^2, \eta) p(\theta_i, \sigma_i^2, \eta)\]

The specimen response \(\mathbf{y}_i\) depends solely on the model parameters \(\theta_i\) and the prediction error variance for that specimen, \(\sigma_i^2\), and is independent of the hyperparameters \(\eta\). Consequently, the conditional PDF \(p(\mathbf{y}_i | \theta_i, \sigma_i^2, \eta)\) reduces to \(p(\mathbf{y}_i | \theta_i, \sigma_i^2)\).

Assuming \(\sigma_i^2\) to be statistically independent of \(\theta_i\) and \(\eta\) in the joint prior PDF of \(\theta_i\), \(\sigma_i^2\), and \(\eta\), (3.2.4) becomes

(3.2.5)\[p(\theta_i, \sigma_i^2, \eta | \mathbf{y}_i) \propto p(\mathbf{y}_i | \theta_i, \sigma_i^2) p(\sigma_i^2) p(\theta_i | \eta) p(\eta)\]

In the context of hierarchical Bayesian modeling, the entire experimental dataset from multiple specimens of the same kind, \(\mathbf{Y} = \{\mathbf{y}_1, \mathbf{y}_2, ..., \mathbf{y}_{N_s}\}\), is considered. The model parameters and the prediction error variances for all specimens are assumed to be mutually statistically independent, while the set of model parameter estimates are assumed to be samples from a parent distribution. The figure Fig. 3.2.2 shows the structure of the hierarchical model.

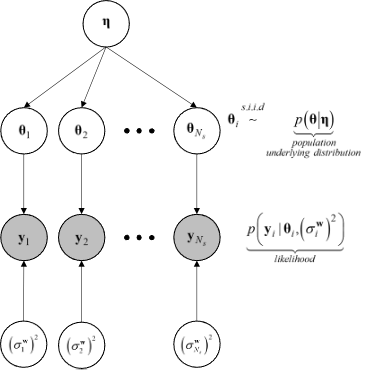
Fig. 3.2.2 Structure of the hierarchical model

Under these assumptions, the equation for Bayesian updating of all unknown quantities in the hierarchical model, including the model parameters \(\Theta = \{\theta_1, \theta_2, \ldots, \theta_{N_s}\}\), measurement noise variances \(\mathbf{s} = \{\sigma_1^2, \sigma_2^2, \ldots, \sigma_{N_s}^2\}\), and hyperparameters \(\eta\) is given by

(3.2.6)\[p(\Theta, \mathbf{s}, \eta | \mathbf{Y}) \propto p(\eta) \prod_{i=1}^{N_s}[p(\mathbf{y}_i | \theta_i, \sigma_i^2) p( \sigma_i^2) p(\theta_i | \eta) ]\]

The marginal posterior distribution of the hyperparameters, \(p(\eta | \mathbf{Y})\) , is obtained by marginalizing out \(\mathbf{\Theta}\) and \(\mathbf{s}\) from \(p(\Theta, \mathbf{s}, \eta | \mathbf{Y})\) as

(3.2.7)\[p(\eta | \mathbf{Y}) = \int_{\Theta, \mathbf{s}} p(\Theta, \mathbf{s}, \eta | \mathbf{Y}) d\Theta d\mathbf{s}\]

The distribution \(p(\eta | \mathbf{Y})\) describes the epistemic uncertainty in the value of the hyperparameters \(\eta\) due to the finite number of specimens \(N_s\) in the experimental dataset.

In the hierarchical approach, the probability distribution of the model parameters conditioned on the entire measurement dataset, \(p(\theta | \mathbf{Y})\), is given by

(3.2.8)\[p(\theta | \mathbf{Y}) = \int_\eta p(\theta | \eta) p(\eta | \mathbf{Y}) d\eta\]

The conditional distribution \(p(\theta | \eta)\) models the aleatory specimen-to-specimen variability. Therefore, the probability distribution \(p(\theta | \mathbf{Y})\), referred to as the posterior predictive distribution of the model parameters \(\theta\), encompasses both the aleatory specimen-to-specimen uncertainty and the epistemic estimation uncertainty (due to the finite number of specimens \(N_s\) in the experimental dataset and the finite length of the experimental data corresponding to each specimen). It can be utilized for uncertainty quantification and propagation in reliability and risk analyses.

Special Case: Normal Population Distribution

The hierarchical modeling approach discussed above captures the specimen-to-specimen aleatory variability by modeling the model parameters corresponding to each experiment as a realization from a population distribution. In the UCSD_UQ engine, a multivariate normal distribution \(\theta | \eta \sim N (\mu_\theta, \Sigma_\theta)\) is adopted (i.e., \(\eta = (\mu_\theta, \Sigma_\theta)\)) as:

(3.2.9)\[\begin{split}\theta_i & \stackrel{s.i.i.d}{\sim} N (\mu_\theta, \Sigma_\theta), \quad i = 1, \ldots, N_s \\ \mu_\theta = \begin{bmatrix} \mu_{\theta_1} \\ \mu_{\theta_2} \\ \vdots \\ \mu_{\theta_{n_\theta}}\end{bmatrix}; \quad \Sigma_\theta &= \begin{bmatrix} \sigma_{\theta_1}^2 & cov(\theta_1, \theta_2) & \cdots & cov(\theta_1, \theta_{n_\theta}) \\ cov(\theta_2, \theta_1) & \sigma_{\theta_2}^2 & \cdots & cov(\theta_2, \theta_{n_\theta}) \\ \vdots & \vdots & \ddots & \vdots \\ cov(\theta_{n_\theta}, \theta_1) & cov(\theta_{n_\theta}, \theta_2) & \cdots & \sigma_{n_\theta}^2 \end{bmatrix}\end{split}\]

In the Bayesian inference process, the hyperparameters characterizing the population probability distribution, the hypermean vector \(\mu_\theta\) and the hypercovariance matrix \(\Sigma_\theta\) are jointly estimated with all the \(\theta_i\) s and \(\sigma_i^2\) s.

So, for this special case, (3.2.6) becomes

(3.2.10)\[p(\Theta, \mathbf{s}, \mu_\theta, \Sigma_\theta | \mathbf{Y}) \propto p(\mu_\theta, \Sigma_\theta) \prod_{i=1}^{N_s}[p(\mathbf{y}_i | \theta_i, \sigma_i^2) p(\sigma_i^2) p(\theta_i | \mu_\theta, \Sigma_\theta) ]\]

with \(\Theta\), \(\mathbf{Y}\), and \(\mathbf{s}\) as defined above.

In the UCSD_UQ engine, the sampling algorithm operates in the standard normal space i.e.,

(3.2.11)\[\begin{split}\theta_i & \stackrel{s.i.i.d}{\sim} N (\mu_\theta, \Sigma_\theta), \quad i = 1, \ldots, N_s \\ \mu_\theta & = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0\end{bmatrix}; \quad \Sigma_\theta = \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{bmatrix}\end{split}\]

and the Nataf transform is utilized to map the values provided by the sampling algorithm to the physical space of the model parameters before the model is evaluated.

Sampling the Posterior Probability Distribution of the Parameters of the Hierarchical Model

Due to the high dimensionality (\(n_\theta \times n_s + n_s + n_\theta + n_\theta \times \frac{(n_\theta+1)}{2}\), corresponding to the dimensions of the \(\theta_i\) of each dataset, \(\sigma_i^2\) for each dataset, \(\mu_\theta\) and \(\Sigma_\theta\), respectively) of the posterior joint PDF shown in (3.2.10), the Metropolis within Gibbs algorithm is used to generate samples from the posterior probability distribution. To do this, conditional posterior distributions are derived for blocks of parameters from the joint posterior distribution (3.2.10) of all the parameters of the hierarchical model. The Gibbs sampler generates values from these conditional posterior distributions iteratively. The conditional posterior distributions are lower dimensional than the joint distribution. The assumptions made next result in a few of the conditional posterior distributions being of a form that can be easily sampled from, thereby making it feasible to draw samples from the high-dimensional joint posterior PDF of the hierarchical model.

The prior distributions for each \(\sigma_i^2\) are selected as the inverse gamma (IG) distribution:

(3.2.12)\[p(\sigma_i^2) = IG(\alpha_0, \beta_0)\]

The prior probability distribution for \((\mu_\theta, \Sigma_\theta)\) is chosen to be the normal-inverse-Wishart (NIW) distribution:

(3.2.13)\[p(\mu_\theta, \Sigma_\theta) = N(\mu_\theta | \mu_0, \frac{\Sigma_\theta}{\nu_0}) IW(\Sigma_\theta | \Sigma_0, m_0)\]

With these assumptions, the conditional posterior distributions are the following:

(3.2.14)\[\begin{split}p(\Sigma_\theta &| \mathbf{Y}, \Theta, \mathbf{s}, \mu_\theta) \propto IW(\Sigma_\theta | \Sigma_n, m_n) \\ p(\mu_\theta &| \mathbf{Y}, \Theta, \mathbf{s}, \Sigma_\theta) \propto N(\mu_\theta | \mu_n, \frac{\Sigma_\theta}{\nu_n}) \\ p(\sigma_i^2 &| \mathbf{Y}, \Theta, \mu_\theta, \Sigma_\theta) \propto IG(\alpha_{n_i}, \beta_{n_i})\\ p(\theta_i &| \mathbf{Y}, \mathbf{s}, \mu_\theta, \Sigma_\theta ) \propto p(\mathbf{y}_i | \theta_i, \sigma_i^2) p(\theta_i | \mu_\theta, \Sigma_\theta)\end{split}\]

where:

(3.2.15)\[\begin{split}\nu_n &= \nu_0 + N_s \\ \mu_n &= \frac{(\mu_0 * \lambda_0 + N_s * \bar{\theta})}{\nu_n} \\ \Sigma_n &= \Sigma_0 + S + \frac{\nu_0 * N_s}{\nu_n} \times ((\bar{\theta} - \mu_0)(\bar{\theta} - \mu_0)^T) \\ m_n &= m_0 + N_s \\ \alpha_{n_i} &= \alpha_0 + \frac{n_{\mathbf{y}_i}}{2}\\ \beta_{n_i} &= \beta_0 + \frac{{sse}_i}{2}\end{split}\]

and,

(3.2.16)\[\begin{split}\bar{\theta} &= \frac{1}{N_s}\sum_{i=1}^{N_s} \theta_i \\ S &= \sum_{i=1}^{N_s} {(\bar{\theta} - \mu_0)(\bar{\theta} - \mu_0)^T} \\ {sse}_i &= \sum_{k=1}^{n_{\mathbf{y}_i}}(\mathbf{y}_i^{(k)} - \mathbf{h}(\theta_i)^{(k)})^2\end{split}\]

The Metropolis within Gibbs sampler generates values from the posterior joint PDF shown in (3.2.10) using the posterior conditional distributions (3.2.14) through the following steps:

1. Select appropriate initial values for each of the \(\theta_i\).

2. Based on the \(k^{th}\) sample value, the \((k+1)^{th}\) sample value is obtained using the following steps:

   1. Generate a sample value of \(\Sigma_{\theta}^{(k+1)}\) from the conditional posterior distribution \(IW(\Sigma_n, m_n)\)

   2. Generate a sample value of \(\mu_\theta^{(k+1)}\) from the conditional posterior distribution \(N(\mu_n, \frac{\Sigma_\theta}{\nu_n})\)

   3. For each dataset, generate independently a sample value of \(\sigma_i^{2(k+1)}\) from the conditional posterior distribution of each \(\sigma_i^2\): \(IG(\alpha_n, \beta_n)\)

   4. For each dataset, generate a sample value of the model parameters \(\theta_i\) from the conditional posterior \(p(\mathbf{y}_i | \theta_i, \sigma_i^2) p(\theta_i | \mu_\theta, \Sigma_\theta)\) with a Metropolis-Hastings step as follows:

      1. Generate a candidate sample \(\theta_{i(c)}\) from a local random walk proposal density \(\theta_{i(c)} \sim N(\theta_i^{(k)}, \Sigma_i^{(k)})\) where \(\Sigma_i^{(k)}\) is the proposal covariance matrix of the random walk.

      2. Calculate the acceptance ratio

      (3.2.17)\[a_c = \frac{p(\mathbf{y}_i | \theta_{i(c)}, \sigma_i^{2(k+1)}) p(\theta_{i(c)} | \mu_\theta^{(k+1)}, \Sigma_{\theta}^{(k+1)})}{p(\mathbf{y}_i | \theta_i^{(k)}, \sigma_i^{2(k+1)}) p(\theta_i^{(k)}| \mu_\theta^{(k+1)}, \Sigma_{\theta}^{(k+1)})}\]

      3. Generate a random value \(u\) from a uniform distribution on [0, 1] and set

      (3.2.18)\[\begin{split}\theta_i^{(k+1)} = \quad &\theta_{i(c)} \quad \text{if} \quad u < a_c \\ &\theta_i^{(k)} \quad \text{otherwise}\end{split}\]

After an initial burn-in period, the sample values generated by this algorithm converge to the target density. The proposal covariance matrix of the random walk \(\Sigma_i^{(k)}\) is selected to facilitate proper mixing of the random walks used to generate sample values of the \(\theta_i\). Within the adaptation duration, a scaled version of the covariance matrix of the sample values of the last \(N_{cov}\) samples (defined as the adaptation frequency in the UCSD_UQ engine) is used, to keep the acceptance rate in the range of 0.2 to 0.5.